在游戏世界里,数学期望是极为关键的一环;它能帮助玩家清晰了解各种技能和招式对伤害量的提升作用;而在运用不同策略时,伤害结果可能会有很大的不同。
数学期望基础概念

数学期望并非直接体现伤害,而是基于多次实验得出的平均伤害值。例如,某技能有50%的概率造成3点伤害,另有50%的概率造成1点伤害,因此该技能的数学期望伤害计算为0.5乘以3加上0.5乘以1,得出的结果是2。在游戏战斗中,玩家可以利用数学期望来预估技能伤害,这有助于他们更好地选择合适的武学和装备。
单次攻击伤害构成
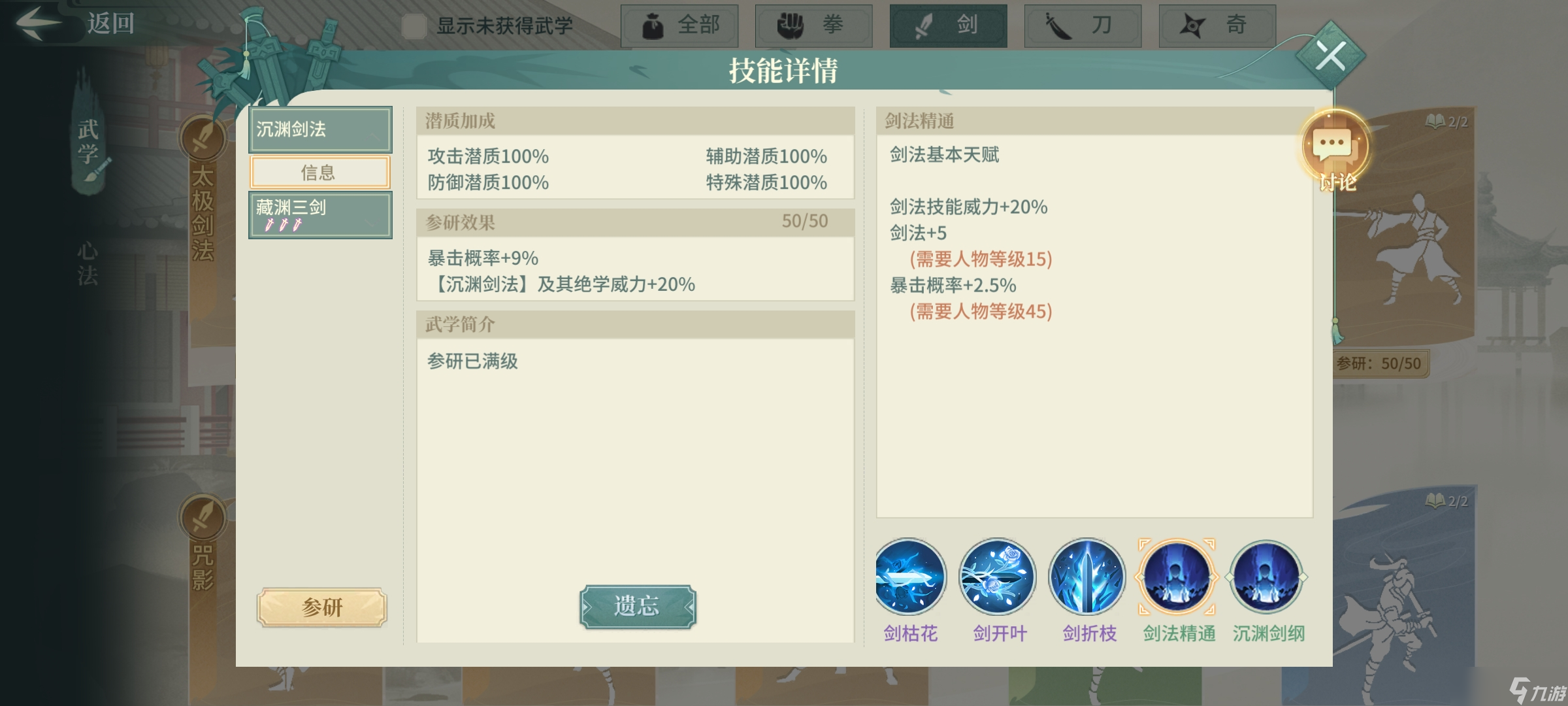
在常规攻击中,伤害值是由攻击力与防御力之差相乘,再与攻击力、攻击波动以及暴击伤害的数值相乘得出的。举例来说,在实际战斗中,玩家可以直观地看到这些因素是如何影响最终伤害的。非暴击时,伤害数值不会提升;但若处于暴击状态,伤害值将增至原数的255%;具体计算,数学期望值是0.872乘以2.55,结果为2.2236;换言之,伤害增加了222.36%。了解这些信息,对于评估技能的输出效果大有裨益。
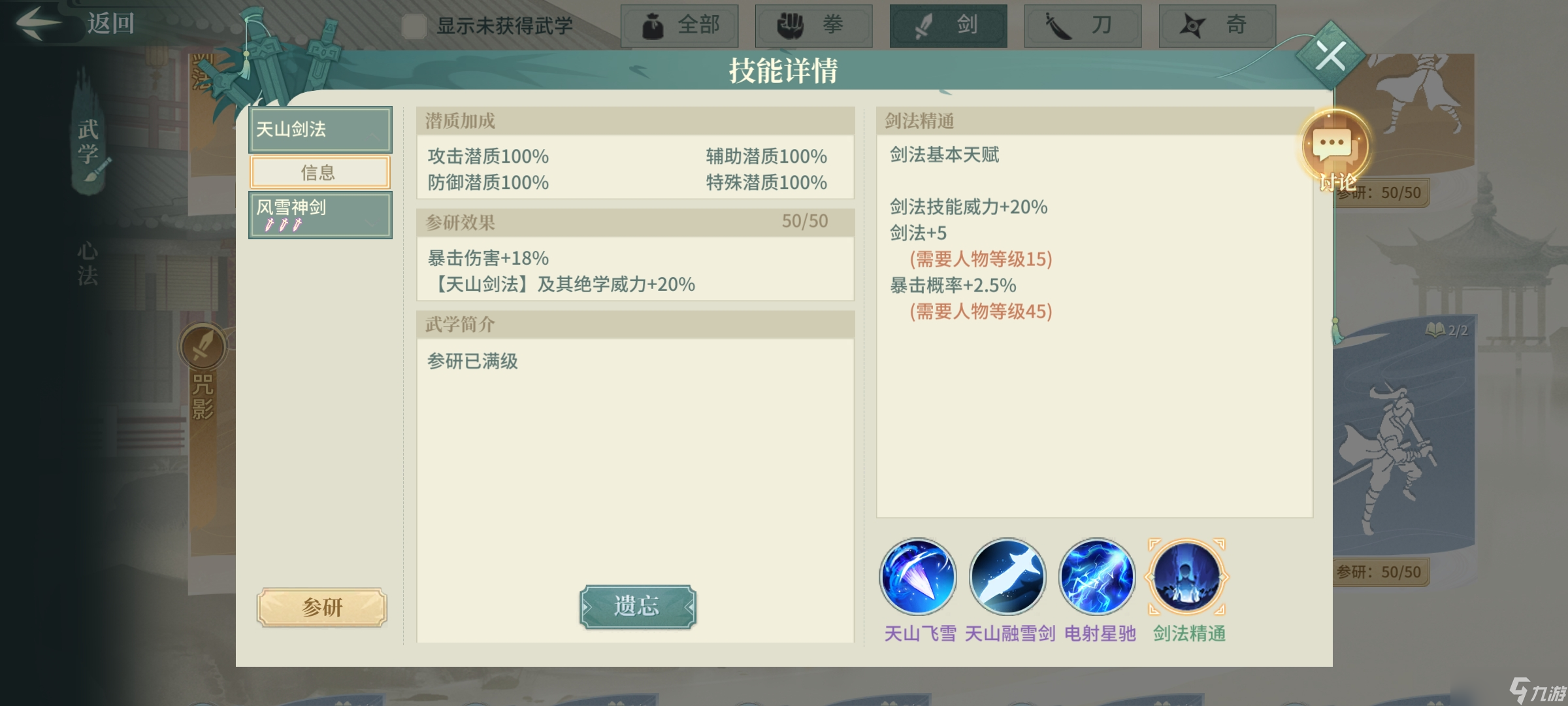
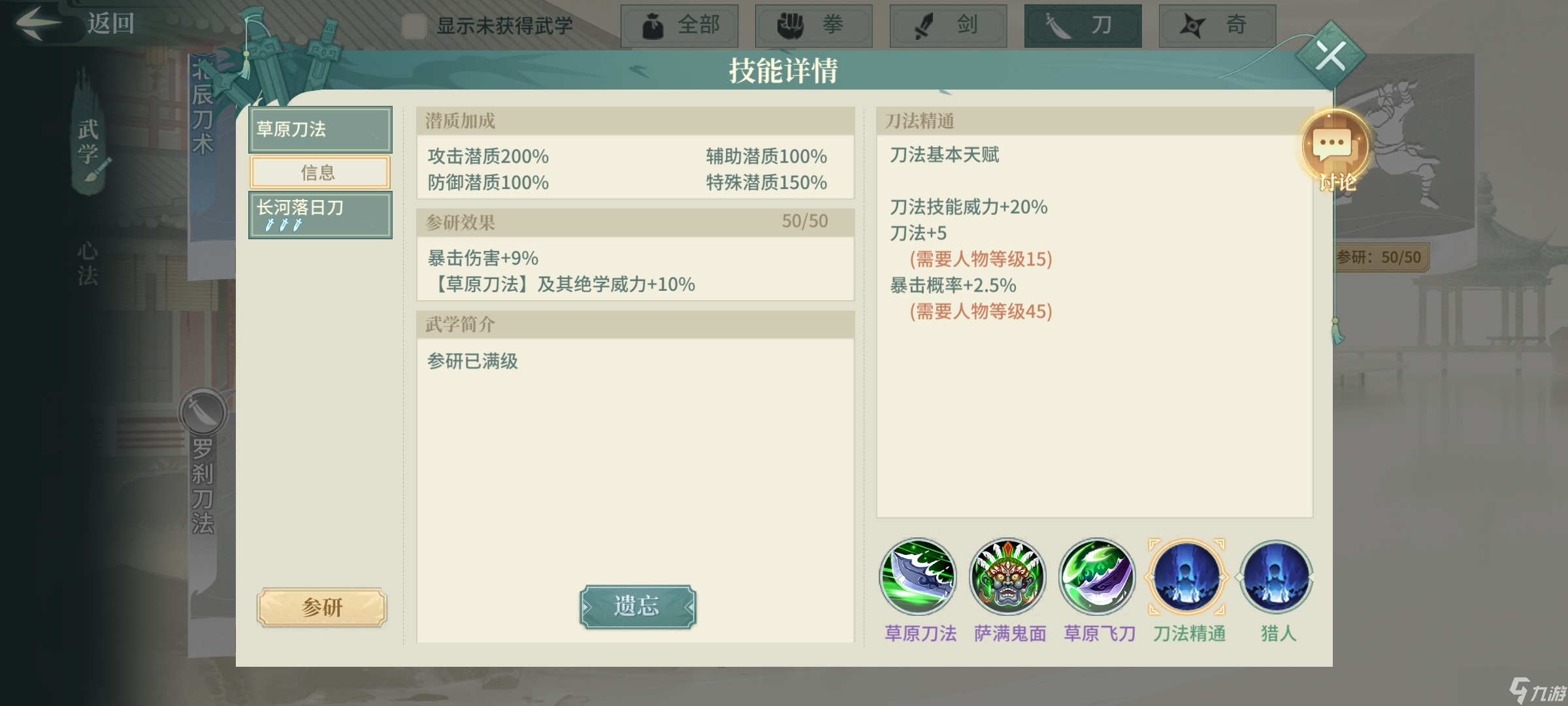
特定武学增伤期望
根据计算结果,沉渊剑法的伤害提升预期高达22.95%。在挑选最后一门武学时,是否应该选择它,确实需要仔细考虑。天风剑法能够发动23%的双击效果,但连续攻击的伤害提升预期需要单独计算。具体来说,E爆的预期伤害是0.23乘以0.6再乘以2.2236,而E不爆的预期伤害则是0.23乘以0.6,等于0.138。由于不同武学的增伤期望各不相同,因此我们需要全面考虑。
不确定数值期望计算
数学期望的不确定性数值计算公式标记为E,其计算方法为(攻击力减去防御力)与威力期望、波动期望、暴击期望、连击期望以及增伤期望相乘。以追命为例,在PVE模式中,其数学期望的威力值为50%;相对地,奋战在PVE模式中的数学期望威力值几乎为零。至于总威力期望的计算,需将各个单项的威力期望值相加,并且在此基础上额外增加100%,但在PVP模式中,这一额外增加的威力将减半。
关键因素期望计算
连击的成功率难以精确估算,这涉及到优先级的考量。以20%的三连击成功率和20%的二连击成功率为例,将它们相加,三连击的成功率仍为20%,而二连击的成功率则降至16%。通常情况下,角色的波动期望值是波动上限和波动下限的平均数,多数武学的波动期望值普遍保持在100%。若某门武术存在基础上的波动,譬如秋水剑的波动阈值增加了10个百分点,那么它的预期效果便会转变为105%。
最终增伤期望情况
在最终的增伤效果里,承影心诀能带来25%的增长,混元手套贡献了15%的增幅,张少爷的火炮则有12%的加成(不过存在一个bug),将这三者相加,当它们都激活时,总的增伤系数是1.25乘以1.15再乘以1.12,得出的结果是1.61。除此之外,还有七星玉真天赋这样的增伤机制。某些特殊状态,例如魔神酒,能够提供100%的暴击概率以及20%的额外爆伤增益,这些因素无疑会对预期的伤害效果造成影响。
看到这里,大家可能心里会琢磨,在实际的游戏操作中,按照这些数学预测来搭配武功和装备,能否实现伤害输出的最大化?不妨给这篇文章点个赞,转发一下,然后在评论区分享您的观点,让我们共同来聊聊这个话题!